Question

NO LINKS!! Each table below represents an exponential function of the form y = ab^x. Complete each table and find the corresponding equation.​

Answer 1

`\textsf{a)} \quad y=1.8(3.2)^x`

`\textsf{b)} \quad y=5(7)^x`

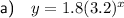
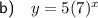
Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

Part (a)

Given ordered pairs:

• (0, 1.8)
• (1, 5.76)
• (2, 18.432)

The y-intercept is the y-value when x = 0.

Therefore, as the y-intercept is 1.8, a = 1.8.

`\implies y=1.8b^x`

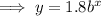
Substitute point (1, 5.76) into the equation and solve for b:

`\begin{aligned} y&=1.8b^x\\\implies 5.76&=1.8 \cdot b^1\\5.76&=1.8b\\b&=(5.76)/(1.8)\\b&=3.2\end{aligned}`

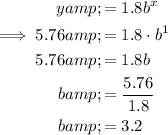
Therefore, the exponential equation is:

`\boxed{y=1.8(3.2)^x}`

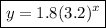
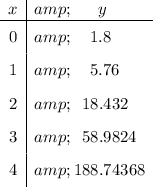
To complete the given table, simply substitute the values of x into the found equation:

`\begin{array}cx&\phantom{189}y\\\cline{1-2} \vphantom{\frac12}}0&\phantom{18}1.8\\\vphantom{\frac12}}1&\phantom{18}5.76\\\vphantom{\frac12}}2&\phantom{1}18.432\\\vphantom{\frac12}}3&\phantom{1}58.9824\\\vphantom{\frac12}}4&188.74368\end{array}`

Part (b)

Given ordered pairs:

• (0, 5)
• (2, 245)

The y-intercept is the y-value when x = 0.

Therefore, as the y-intercept is 5, a = 5.

`\implies y=5b^x`

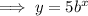
Substitute point (2, 245) into the equation and solve for b:

`\begin{aligned} y&=5b^x\\\implies 245&=5 \cdot b^2\\49&=b^2\\b&=√(49)\\b&=7\end{aligned}`

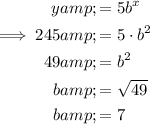
Therefore, the exponential equation is:

`\boxed{y=5(7)^x}`

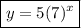
To complete the given table, simply substitute the values of x into the found equation:

`\begin{array}lx&\phantom{11}y\\\cline{1-2} \vphantom{\frac12}}0&\phantom{1111}5\\\vphantom{\frac12}}1&\phantom{111}35\\\vphantom{\frac12}}2&\phantom{11}245\\\vphantom{\frac12}}3&\phantom{1}1715\\\vphantom{\frac12}}4&12005\end{array}`