Question

10 Find the value of 2x+y for the simultaneous equations.
3x + 5y = 48
2x-y=19

Answer 1

y=3

x=11

hence answer 25

3x+5y=48

2x-y=19

eliminate x to find y

(3x+5y=48)2

(2x-y=19)3

(6x + 10y. = 96)

- minus direct

(6x - 3y. = 57)

=

13y = 39

Note: (10y -(-3y)=13y)

divide by 13 to remain with y

y =3

substitute to any equation to get x lets pick second one

2x-(3)=19

2x-3=19

2x=19+3

2x/2=22/2. (to remain with x value)

x=11

therefore 2x+ y results to 2(11) +3=25

Answer 2

2x + y = 25

Explanation:

Given equations:

`\begin{cases} 3x + 5y = 48\\\;\;2x-y=19\end{cases}`

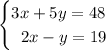
Rearrange the second equation to isolate y:

`\implies 2x-y=19`

`\implies 2x-19=y`

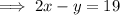
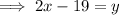
Substitute the found expression for y into the first equation and solve for x:

`\implies 3x+5y=48`

`\implies 3x+5(2x-19)=48`

`\implies 3x+10x-95=48`

`\implies 13x=143`

`\implies x=11`

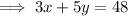
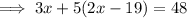
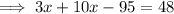
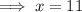
Substitute the found value of x into the equation for y and solve for y:

`\implies y=2x-19`

`\implies y=2(11)-19`

`\implies y=22-19`

`\implies y=3`

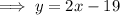
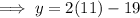
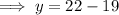
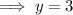
Therefore, the solution of the given system of equations is:

• x = 11, y = 3

To find the value of 2x + y, substitute the found values of x and y into the expression and solve:

`\begin{aligned}\implies 2x+y&=2(11)+3\\&=22+3\\&=25\end{aligned}`

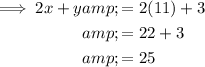
Therefore:

• 2x + y = 25