Question

X²y²+4x+6y-5=0 and (x+2)²=2(y+1) what value do you get for y

Answer 1

The value of x+2y is 10.

Let's work through the given equations:

`y =y^x\\x^2=y`

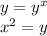
From equation 2, we can substitute y in equation 1 with
`x^2` :

`y =y^x\\x^2 =(x^2 )^x\\x^2 =x^(2x)`

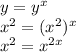
For these exponents to be equal, their bases must be the same:

`x^2 =2x`

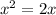
Rearranging this equation gives us two possible solutions for x:

x=0 (which we discard because

x and y are distinct positive real numbers)

x=2

From equation 2, if x=2, then
`y=x^2 =2^2 =4.`

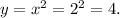
Therefore, x=2 and y=4.

Finally, substitute these values into x+2y:

x+2y=2+2×4=2+8=10

So, x+2y=10.

Question

If x^y=y^x and x^2=y, and x and y are distinct positive real numbers, then what is the value of x+2y?