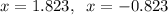Question

I can't theme to grasp these questions can someone please explain the steps ?

Answer 1

(i) See below for proof.

(ii) x = 1.823, x = -0.823

Explanation:

Part (i)

Given equation:

`(x+2)/(x+1)+(3)/(x)=3`

Make the denominators of the fractions the same:

`\implies (x+2)/(x+1)\cdot (x)/(x)+(3)/(x)\cdot (x+1)/(x+1)=3`

`\implies (x(x+2))/(x(x+1))+(3(x+1))/(x(x+1))=3`

`\textsf{Apply the fraction rule} \quad (a)/(c)+(b)/(c)=(a+b)/(c):`

`\implies (x(x+2)+3(x+1))/(x(x+1))=3`

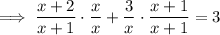
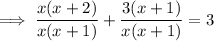
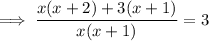
Multiply both sides of the equation by x(x + 1) to eliminate the denominator of the fraction on the LHS:

`\implies x(x+2)+3(x+1)=3x(x+1)`

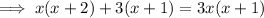
Expand the brackets:

`\implies x^2+2x+3x+3=3x^2+3x`

`\implies x^2+5x+3=3x^2+3x`

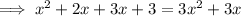
Subtract x² from both sides:

`\implies 5x+3=2x^2+3x`

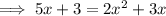
Subtract 5x from both sides:

`\implies 3=2x^2-2x`

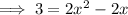
Subtract 3 from both sides:

`\implies 0=2x^2-2x-3`

`\implies 2x^2-2x-3=0`

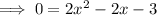
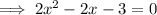
Part (ii)

`\boxed{\begin{minipage}{3.6 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

To solve the quadratic equation
`2x^2-2x-3=0`, use the quadratic formula.

Therefore:

• a = 2
• b = -2
• c = -3

Substitute these values into the formula and solve for x:

`\implies x=(-(-2) \pm √((-2)^2-4(2)(-3)))/(2(2))`

`\implies x=(2 \pm √(4+24))/(4)`

`\implies x=(2 \pm √(28))/(4)`

`\implies x=(2 \pm √(4 \cdot 7))/(4)`

`\implies x=(2 \pm √(4) √(7))/(4)`

`\implies x=(2 \pm 2 √(7))/(4)`

`\implies x=(1 \pm √(7))/(2)`

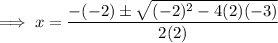
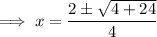
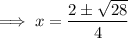
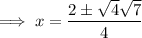
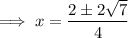
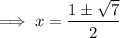
Therefore, the solutions correct to 3 decimal places are:

`x=1.823,\;\; x= -0.823`