Question

PLEASE ILL DO ANYTHING I ALREADY OFFERED AS MUCH POINTS AS POSSIBLE

Answer 1

A, B, D, E

Explanation:

Given expression:

• (0.06) · (0.154)

When multiplying decimals, multiply as if there are no decimal points:

`\implies 6 * 154 = 924`

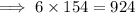
Count the number of digits after the decimal in each factor:

• 0.06 → 2 digits

• 0.154 → 3 digits

Therefore, there is a total of 5 digits.

Put the same number of total digits after the decimal point in the product:

`\implies (0.06) \cdot (0.154)=0.00924`

-----------------------------------------------------------------------------------------------

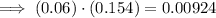
Answer option A

`\boxed{6 \cdot (1)/(100) \cdot 154 \cdot (1)/(1000)}`

When dividing by multiples of 10 (e.g. 10, 100, 1000 etc.), move the decimal point to the left the same number of places as the number of zeros.

Therefore:

• 6 ÷ 100 = 0.06
• 154 ÷ 1000 = 0.154

`\implies 6 \cdot (1)/(100) \cdot 154 \cdot (1)/(1000)=(0.06) \cdot (0.154)`

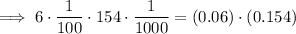
Therefore, this is a valid answer option.

Answer option B

`\boxed{6 \cdot 154 \cdot (1)/(100000)}`

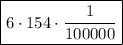
Multiply the numbers 6 and 154:

`\implies 6 * 154 = 924`

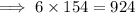
Divide by 100,000 by moving the decimal point to the left 5 places (since 100,000 has 5 zeros).

`\implies 6 \cdot 154 \cdot (1)/(100000)=0.00924`

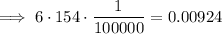
Therefore, this is a valid answer option.

Answer option C

`\boxed{6 \cdot (0.1) \cdot 154 \cdot (0.01)}`

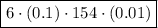
Again, employ the technique of multiplying decimals by first multiplying the numbers 6 and 154:

`\implies 6 \cdot 154 = 924`

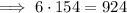
Count the number of digits after the decimal in each factor:

• 0.1 → 1 digit

• 0.01 → 2 digits

Therefore, there is a total of 3 digits.

Put the same number of digits after the decimal point in the product:

`\implies 0.924`

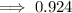
Therefore, as (0.06) · (0.154) = 0.00924, this answer option does not equal the given expression.

Answer option D

`\boxed{6 \cdot 154 \cdot (0.00001)}`

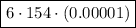
Again, employing the technique of multiplying decimals.

As there are a total of 5 digits after the decimals:

`\implies 6 \cdot 154 \cdot (0.00001)=0.00924`

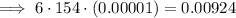
Therefore, this is a valid answer option.

Answer option E

`\boxed{0.00924}`

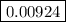
As we have already calculated, (0.06) · (0.154) = 0.00924.

Therefore, this is a valid answer option.