Question

What is the area of rectangle FGHI?

Answer 1

58

Explanation:

Here, we are given rectangle FGHI and we want to find the area.

To do so we must first find the lengths of the sides and then we can calculate the area using the formula "area = length x width"

Finding the side lengths.

We can find the lengths of the sides by using the distance formula
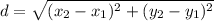`d=√((x_2-x_1)^2+(y_2-y_1)^2)` where (x1,y1) and (x2,y2) are from the points of the line. To make it easier its best to list the coordinates of the vertices.

• F : (3,5)
• I : (8,3)
• H : (4,-7)
• G : (-1,-5)

Finding the length of segment FI

Given coordinates of F and I are (3,5) and (8,3)

Defining our variables, we get (x1,y1) = (3,5) and (x2,y2) = (8,3)

This means that x1 = 3 , y1 = 5, x2 = 8 and y2= 3

We now want to plug these values into the formula

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

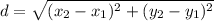
==> plug in x1 = 3 , y1 = 5, x2 = 8 and y2= 3

`d=√((8-3)^2+(3-5)^2)`

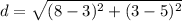
==> simplify subtraction

`d=√((5)^2+(-2)^2)`

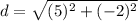
==> evaluate exponents

`d=√(25+4)`

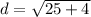
==> simplify addition

`d=√(29)`

So the side width or smaller side has a length of √29

Finding the length of segment IH

Given coordinates of I and H are (8,3) and (4,-7)

Defining our variables we get (x1,y1) = (8,3) and (x2,y2) = (4,-7)

This means that x1 = 8, y1 = 3, x2 = 4 and y2 = -7

We now plug in these values into the formula

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

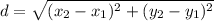
==> plug in x1 = 8, y1 = 3, x2 = 4 and y2 = -7

`d=√((4-8)^2+(-7-3)^2)`

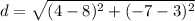
==> simplify subtraction

`d=√((-4)^2+(-10)^2)`

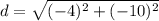
==> evaluate exponents

`d=√(16+100)`

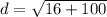
==> simplify addition

`d=√(116)`

==> simplify radical

`d= 2√(29)`

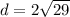
So the length of IH is 2√29

Finding the area

Now that we have the lengths of the sides of the rectangle we can find the area of the rectangle.
We know that the area of a rectangle is equivalent to the length multiplied by the width.

Here, we've identified that the length is 2√29 and the width is √29

This means that the area would be :

`2√(29) *√(29)`

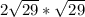
==> simplify using the rule :
`b√(a)*√(a)=b√(a^2) =b(a)`

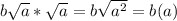
2(29)

==> multiply 2 and 29

=58

The area of the rectangle is 58