Question

Many people use scanners to read documents and store them into pdf file. To help determine which brand of scanner to buy, a student conducts an experiment in which 8 different documents were scanned by each of the two scanners that he is interested in. He records the number of errors made by each. Can he infer that Brand A (the more expensive scanner) is better than Brand B

Answer 1

To determine if Brand A is better than Brand B, statistical analysis can be used. Calculate the mean number of errors made by each scanner and perform a two-sample t-test.

Step-by-step explanation:

In order to determine if Brand A is better than Brand B, the student conducted an experiment where 8 different documents were scanned by each scanner. The number of errors made by each scanner was recorded. To infer if Brand A is better than Brand B, statistical analysis can be used.

First, calculate the mean number of errors made by each scanner. Then, perform a two-sample t-test to compare the means of the two scanners. If the p-value from the t-test is less than a predefined significance level (e.g., 0.05), it can be concluded that there is a statistically significant difference in the number of errors between the two scanners.

However, it's important to note that the cost of a scanner does not necessarily determine its quality. Other factors such as features, durability, and customer reviews should also be considered when making a purchasing decision.

Answer 2

The data is missing in the question. The data is provided below :

Document : 1 2 3 4 5 6 7 8

Brand A 17 29 18 14 21 25 22 29

Brand B 21 38 15 19 22 30 31 37

Solution :

State of the hypothesis of the null hypothesis and alternate hypothesis.

Null hypothesis :
`$h_A = h_B$`

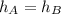
Alternate hypothesis :
`$h_A > h_B$`

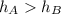
These hypothesis is a one tailed test. The null hypothesis will get rejected when the mean difference between the sample means is very small.

Significance level = 0.05

Therefore the standard error is :
`$SE = \sqrt{((s^2_1)/(n_1))+((s^2_2)/(n_2))}$`

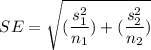
= 3.602

And the degree of freedom, DF = 14

`$t=((x_1-x_2)-d)/(SE)$`

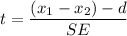
= -1.319

Here,
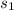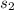`$s_1$` = standard deviation of the sample 1

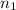`$s_2$` = standard deviation of the sample 2

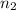`$n_1$` = size of the sample 1

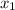`$n_2$` = size of the sample 2

`$x_1$` = mean of the sample 1

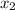`$x_2$` = mean of the sample 2

d = the hypothesis difference between the population mean

The observed difference in a sample means t static of -1.32. From t distribution calculator to determine P(
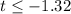`$t \leq -1.32$`) = 0.1042

Since the P value of 0.1042 is greater than significance level o 0.05, we therefore cannot reject the null hypothesis.

But from the test, we have no sufficient evidence that supports that Brand A is better than Brand B.