Question

Find the center of mass of a rectangular block of length a and width b that has a nonuniform density such that when the rectangle is placed in the x,y-plane with one corner at the origin and the block placed in the first quadrant with the two edges along the x- and y-axes, the density is given by rho(x,y)=rho0x, where rho0 is a constant.

a) (a/2, b/2)
b) (a/3, b/3)
c) (a/4, b/4)
d) (a, b)

Answer 1

The center of mass of a rectangular block of length a and width b will be c) (a/4, b/4)

Step-by-step explanation:

To find the center of mass (CM) of the rectangular block with nonuniform density ρ(x, y) = ρ₀x, we'll use the formulas for the x- and y-coordinates of the center of mass. For a two-dimensional object, the x-coordinate (Xcm) and y-coordinate (Ycm) are given by:

`\[X_(cm) = (1)/(M) \int_(A) x \cdot \rho(x, y) \, dA\]`

`\[Y_(cm) = (1)/(M) \int_(A) y \cdot \rho(x, y) \, dA\]`

Here, M is the mass of the object, and the integrals are taken over the area A of the object. The density function is given by ρ(x, y) = ρ₀x.

Integrating over the area of the rectangle with vertices (0, 0), (a, 0), (a, b), and (0, b), we find the mass M as:

`\[M = \int_(0)^(b) \int_(0)^(a) \rho(x, y) \, dx \, dy = \int_(0)^(b) \int_(0)^(a) \rho₀x \, dx \, dy = (1)/(2) \rho₀ab^2\]`

Now, we apply these values to find the center of mass coordinates:

`\[X_(cm) = (1)/((1)/(2) \rho₀ab^2) \int_(0)^(b) \int_(0)^(a) x \cdot \rho(x, y) \, dx \, dy\]`

`\[Y_(cm) = (1)/((1)/(2) \rho₀ab^2) \int_(0)^(b) \int_(0)^(a) y \cdot \rho(x, y) \, dx \, dy\]`

Evaluating these integrals yields
`\(X_(cm) = (a)/(4)\) and \(Y_(cm) = (b)/(4)\)`, giving the center of mass coordinates as
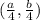`\(((a)/(4), (b)/(4))\)`. Therefore, the correct answer is (c).