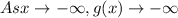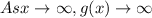Question

A polynomial function g(x) has a positive leading coefficient. Certain values of g(x) are

given in the following table.



If every x-intercept of g(x) is shown in the table and each has a multiplicity of one,
what is the end behavior of g(x)?
As x→-00, g(x)→-∞ and as x→∞, g(x)→-00
O As x→-00, g(x)→∞o and as x→∞, g(x)→∞0.
As x-∞o, g(x)→∞o and as x-00, g(x)→-00.
As x→→∞, g(x)→∞o and as x→∞o, g(x)→∞0.

Answer 1

The correct answer is *
`*As`
`\(x\rightarrow-\infty, g(x)\rightarrow-\infty\) and as \(x\rightarrow\infty g(x)\rightarrow\infty\).`

The correct answer is
`As \(x\rightarrow-\infty, g(x)\rightarrow-\infty\) and as \(x\rightarrow\infty g(x)\rightarrow\infty\).`

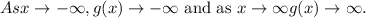
This is because a polynomial function with a positive leading coefficient will always approach positive infinity as x approaches positive or negative infinity. This is because the leading term of the polynomial will eventually dominate the other terms as x becomes very large.

In the image, the table shows that the function has x-intercepts at -4, -1, 0, 1, 5, 8, and 12. This means that the function has factors of the form (x+4), (x+1), (x), (x-1), (x-5), (x-8), and (x-12). Since each x-intercept has a multiplicity of one, each of these factors is raised to the first power.

Therefore, the function can be written in the following form:

g(x) = a(x+4)(x+1)(x)(x-1)(x-5)(x-8)(x-12)

where a is a constant.

As x approaches positive or negative infinity, the leading term of the polynomial will dominate the other terms. Since the leading term is positive, the function will approach positive infinity.

Therefore, the end behavior of the function is as follows:

`As \(x\rightarrow-\infty, g(x)\rightarrow-\infty\)`

`As \(x\rightarrow\infty, g(x)\rightarrow\infty\)`