Question

9) An airplane turns by "banking"; if it's at constant speed, thethrust force from the propellers (or jet engines) just cancels thedrag force resisting the direction of motion. The remaining forcesare the lift force, which is perpendicular to the wings, and gravity.A) While the plane is banking, describe the origin of the centripetalforce that makes the airplane turn in a large horizontal circle.B) If the plane goes 240 km/hr (the cruising speed of the ~1930Ford Trimotor pictured) and the bank angle shouldn't exceed 35 degrees, what is the minimum turning radius (radius of thecircle it will make if it turns 360 degrees)?

Answer 1

A) he centripetal force is the radial component of the lift force.

B) r = 647.7 m

Step-by-step explanation:

A) in the problem indicates that we have two forces acting, gravity and the lift force.

The force of gravity on an object is always directed towards the center of the Earth, so it has no effect on a horizontal spin.

The lift force is perpendicular to the wing of the plane and in the vertical direction, therefore if the plane inclines if the wings respect the horizontal, it has a component of the force in the radial direction, this is responsible for the rotation of the plane.

consequently the centripetal force is the radial component of the lift force.

B) let's write Newton's second law, where the reference frame is horizontal x axis

x-axis (radial)

F_s sin θ = m a

acceleration is centripetal

a = v² / r

F_s sin θ = m v² / r

Y xis

F_s cos θ - W = 0

F_s cos θ = mg

the turn is horizontal so there is not y-axis aceleration

we divide the two equations

tan θ = v² / rg

r =
`(v^2)/( g \ tan \theta )`

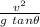
let's veloicity to the SI system

v = 240 km / h (1000m / 1 km) (1h / 3600s) = 66.6667 m / s

let's calculate

r =
`(66.6667^2)/(9.8 \ tan 35)`

r = 647.7 m