Question

Aubrey invested $61,000 in an account paying an interest rate of 1.9% compounded continuously. Assuming no deposits or withdrawals are made, how long would it take, to the nearest tenth of a year, for the value of the account to reach $73,600?

Answer 1

Answer: 9.9 years.

Explanation:

If interest is compounded continuously, then formula to compute final amount A =
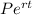`Pe^(rt)`, where P =initial amount, r= rate of interest , t=time.

Given: P= $61,000, r= 1.9% =0.019 , A = $ 73600

Substitute all values in formula

`73600=61000e^(0.019t)\\\\\Rightarrow\ (73600)/(61000)=e^(0.019t)\\\\\Rightarrow\ 1.20655738=e^(0.019t)`

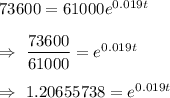
Taking natural log on both sides

`\ln (1.20655738)=0.019t\\\\\\ 0.18777116=0.019t\\\\\\ t=(0.18777116)/(0.019)\\\\\\ t=9.88269263\approx9.9\ \text{years}`

Hence, the required time = 9.9 years.