The initial horizontal component of the pumpkin's velocity is 73.9 m/s. The initial vertical component of the pumpkin's velocity is 51.4 m/s. It takes 5.23 seconds for the pumpkin to reach its maximum height. The maximum height that the pumpkin reaches is 132 meters. The pumpkin travels 388 meters in the x direction.
a. What is the initial horizontal component of the pumpkin's velocity?
To solve this, we can use the following equation:
 =
=
 * cos(theta)
* cos(theta)
where:
 is the initial horizontal component of the pumpkin's velocity
is the initial horizontal component of the pumpkin's velocity
 is the initial velocity of the pumpkin leaving the cannon
is the initial velocity of the pumpkin leaving the cannon
theta is the angle at which the cannon is fired
We know that
 is the same as in problem 13, which is 91 m/s. We also know that theta is 35 degrees. Plugging these values into the equation, we get:
is the same as in problem 13, which is 91 m/s. We also know that theta is 35 degrees. Plugging these values into the equation, we get:
 = 91 m/s * cos(35 degrees) = 73.9 m/s
= 91 m/s * cos(35 degrees) = 73.9 m/s
Therefore, the initial horizontal component of the pumpkin's velocity is 73.9 m/s.
b. What is the initial vertical component of the pumpkin's velocity?
To solve this, we can use the following equation:
 =
=
 * sin(theta)
* sin(theta)
where:
 is the initial vertical component of the pumpkin's velocity
is the initial vertical component of the pumpkin's velocity
 is the initial velocity of the pumpkin leaving the cannon
is the initial velocity of the pumpkin leaving the cannon
theta is the angle at which the cannon is fired
We know that
 is the same as in problem 13, which is 91 m/s. We also know that theta is 35 degrees. Plugging these values into the equation, we get:
is the same as in problem 13, which is 91 m/s. We also know that theta is 35 degrees. Plugging these values into the equation, we get:
 = 91 m/s * sin(35 degrees) = 51.4 m/s
= 91 m/s * sin(35 degrees) = 51.4 m/s
Therefore, the initial vertical component of the pumpkin's velocity is 51.4 m/s.
c. How long does it take for the pumpkin to reach its maximum height le. find the time it takes to reach the peak?
To solve this, we can use the following equation:
 =
=
 / g
/ g
where:
 is the time it takes for the pumpkin to reach its maximum height
is the time it takes for the pumpkin to reach its maximum height
 is the initial vertical component of the pumpkin's velocity
is the initial vertical component of the pumpkin's velocity
g is the acceleration due to gravity (9.81
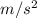 )
)
We know that
 is 51.4 m/s and g is 9.81
is 51.4 m/s and g is 9.81
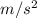 . Plugging these values into the equation, we get:
. Plugging these values into the equation, we get:
 = 51.4 m/s / 9.81
= 51.4 m/s / 9.81
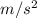 = 5.23 seconds
= 5.23 seconds
Therefore, it takes 5.23 seconds for the pumpkin to reach its maximum height.
d. How high off the ground does the pumpkin go to what is the maximum height?
To solve this, we can use the following equation:
 =
=
 / 2g
/ 2g
where:
 is the maximum height that the pumpkin reaches
is the maximum height that the pumpkin reaches
 is the initial vertical component of the pumpkin's velocity
is the initial vertical component of the pumpkin's velocity
g is the acceleration due to gravity (9.81
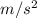 )
)
We know that
 is 51.4 m/s and g is 9.81
is 51.4 m/s and g is 9.81
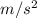 . Plugging these values into the equation, we get:
. Plugging these values into the equation, we get:
 = 51.4
= 51.4
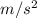 / 2 * 9.81
/ 2 * 9.81
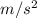 = 132 meters
= 132 meters
Therefore, the maximum height that the pumpkin reaches is 132 meters.
e. How far does the pumpkin go in the x direction?
To solve this, we can use the following equation:
x =
 * t
* t
where:
x is the distance that the pumpkin travels in the x direction
 is the initial horizontal component of the pumpkin's velocity
is the initial horizontal component of the pumpkin's velocity
t is the time that the pumpkin is in the air
We know that
 is 73.9 m/s and t is 5.23 seconds. Plugging these values into the equation, we get:
is 73.9 m/s and t is 5.23 seconds. Plugging these values into the equation, we get:
x = 73.9 m/s * 5.23 seconds
= 388 meters
Therefore, the pumpkin travels 388 meters in the x direction.