Answer:
The correct option is c. 75 for this question
Step-by-step explanation:
The correct option is c. 75 for this question:
Let's see how.
Continuity Equation is given as:
AcVc = AaVa
Where,
Aa = Area of Aorta
Ac = Area of the capillary
Va = Fluid speed in Aorta
Vc = Fluid speed in Capillary
So,
Assuming the fluid is the ideal one/
 /4
/4
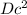 Vc=
Vc=
 /4
/4
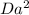 Va
Va
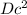 Vc=
Vc=
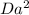 Va
Va
Dc = Da x
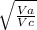
Dc = 2.5 cm x
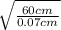
Dc = 73.192 cm
Dc = 75 approximately
Hence, the diameter of the capillary = 75 cm approximately