Question

Please help! Worth 100 points!

What is the length of the hypotenuse? (Hint: Use Pythagoras' theorem.)
What is the sine of x?
What is the cosine of x?
What is the tangent of x?
Write an explanation of SOHCAHTOA as if you are explaining what it represents to a new geometry student. Include at least one diagram. Be thorough.

Answer 1

Hypotenuse = 159 ft (nearest integer)

`\sin(x)=(53)/(159)`

`\cos(x)=(150)/(159)`

`\tan(x)=(53)/(150)`

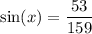
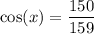
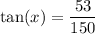
Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

From inspection of the given right triangle:

• a = 53 ft
• b = 150 ft

Substitute these values into Pythagoras Theorem and solve for c (hypotenuse):

`\implies 53^2+150^2=c^2`

`\implies 2809+22500=c^2`

`\implies 25309=c^2`

`\implies c=√(25309)`

`\implies c=159.0880259...`

`\implies c=159\;\; \sf ft\;\;(nearest\;integer)`

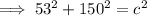
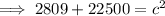
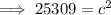
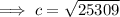
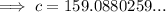
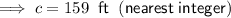
Therefore, the hypotenuse of the given triangle is 159 ft (nearest integer).

-----------------------------------------------------------------------------------------------

Trigonometric ratios

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

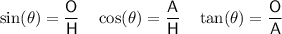
where:

• θ is the angle.
• O is the side opposite the angle.
• A is the side adjacent the angle.
• H is the hypotenuse (the side opposite the right angle).

Given:

• θ = x
• A = 150
• O = 53
• H = 159

Substitute the values into the ratios:

`\implies \sin(x)=(53)/(159)`

`\implies \cos(x)=(150)/(159)`

`\implies \tan(x)=(53)/(150)`

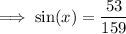
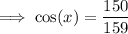
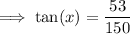
SOHCAHTOA is a mnemonic for the definitions of the trigonometric ratios applicable to right triangles:

• Sine of an angle is equal to Opposite over Hypotenuse.
• Cosine of an angle is equal to Adjacent over Hypotenuse.
• Tangent of an angle is equal to Opposite over Adjacent.

(See attachment).