Question

Mrs Williams has a prize box with different colored tickets as shown below each ticket results in a different type of prize Pedro will randomly select a ticket replacement select another ticket which is the yellow and then a purple

Answer 1

The probability of Pedro randomly selecting a yellow ticket followed by a purple ticket from Mrs. Williams' prize box, with replacement, is
`\( (3)/(25) \)`. This is calculated by multiplying the individual probabilities of each event.

To find the probability of Pedro choosing a yellow ticket and then a purple ticket, we multiply the probabilities of each event because the selections are made with replacement. The total number of tickets is 3 + 4 + 3 = 10.

1. **Probability of choosing a yellow ticket:**

`\[ P(\text{Yellow}) = \frac{\text{Number of yellow tickets}}{\text{Total number of tickets}} = (4)/(10) = (2)/(5) \]`

2. **Probability of choosing a purple ticket:**

`\[ P(\text{Purple}) = \frac{\text{Number of purple tickets}}{\text{Total number of tickets}} = (3)/(10) \]`

Now, multiply the probabilities of each event:

`\[ P(\text{Yellow and then Purple}) = P(\text{Yellow}) * P(\text{Purple}) \]`

`\[ P(\text{Yellow and then Purple}) = (2)/(5) * (3)/(10) \]`

`\[ P(\text{Yellow and then Purple}) = (6)/(50) \]`

Simplify the fraction:

`\[ P(\text{Yellow and then Purple}) = (3)/(25) \]`

Therefore, the correct answer is (a)
`\( (3)/(25) \).`

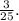
The probable question may be:

Mrs Williams has a prize box with different colored tickets as shown below. each ticket results in a different type of prize. Pedro will randomly select a ticket replace it and then select another ticket. what is the probability that he chooses which a yellow and then a purple ticket? 3 green tickets, 4 yellow tickets, 3 purple tickets. a. 3/25 b. 2/15 c. 4/25 d. 7/20