Question

Adilla invests $1200 at a rate of 2.6% per year compound interest. Calculate the value of her investment at the end of 2 years.

Answer 1

The value of Adilla's investment at the end of 2 years is $1,255.32.

Step-by-step explanation:

To calculate the compound interest, we use the formula:

`A = P * (1 + r/n)^{(nt)`

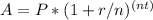
Where:

A is the future value of the investment/loan, including interest.

P is the principal investment amount (the initial deposit or loan amount).

r is the annual interest rate (as a decimal).

n is the number of times that interest is compounded per unit t (usually, n is the number of times per year).

t is the time the money is invested or borrowed for, in years.

In this case, P = $1200, r = 0.026 (2.6% expressed as a decimal), n = 1 (compounded annually), and t = 2 years.

`A = $1200 * (1 + 0.026/1)^{(1 * 2)`

`A = $1200 * (1.026)^2`

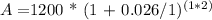
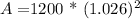
A ≈ $1200 * 1.053476

A ≈ $1255.32

Therefore, the value of Adilla's investment at the end of 2 years is approximately $1,255.32.