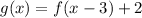Question

Give an equation for the transformation that maps the graph of f onto the graph of g.

Answer 1

Transformations of Graphs

`g(x)=cf(b(x-h))+k`

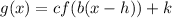
• g(x) is the transformed function
• f(x) is the original function
• c = vertical stretch (negative = reflect about the x-axis)
• b = horizontal stretch (negative = reflect about the y-axis)
• h = horizontal translation (negative = moves left)
• k = vertical translation (negative = moves down)

Solving the Question

We know that only a vertical translation and horizontal translation were applied to the graph. How?

• The slopes of each segment remained the same, indicating that there was no vertical or horizontal stretch

To identify what values of h and k to use, identify the translations applied to one of the points:

(1,2) ⇒ (4,4)

• It moved 3 units right
• It moved 2 units up

Therefore:

• h = 3
• k = 2

Plug this into the equation:

`g(x)=cf(b(x-h))+k\\g(x)=f(x-h)+k\\g(x)=f(x-3)+2`

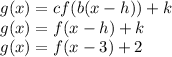
Answer

`g(x)=f(x-3)+2`