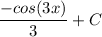Question

Sin (3x) dx = ?
find the integral

Answer 1

`\displaystyle \displaystyle \int {sin(3x)} \, dx = (-cos(3x))/(3) + C`

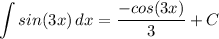
General Formulas and Concepts:

Calculus

Antiderivatives - Integrals

Integration Constant C

Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

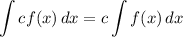
Trig Integration:
`\displaystyle \int{sin(x)} \, dx = -cos(x) + C`

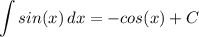
U-Substitution

Explanation:

Step 1: Define

`\displaystyle \int {sin(3x)} \, dx`

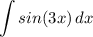
Step 2: Identify Substitution Variables

u = 3x

du = 3dx

Step 3: Integrate

1. [Integral] Rewrite:
   `\displaystyle (1)/(3)\int {3sin(3x)} \, dx`
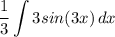
2. [Integral] U-Substitution:
   `\displaystyle (1)/(3)\int {sin(u)} \, du`
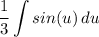
3. [Integral] Trig Integration:
   `\displaystyle (1)/(3)[-cos(u)] + C`
4. [Expression] Multiply:
   `\displaystyle (-cos(u))/(3) + C`
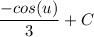
5. [Expression] Back-Substitute:
   `\displaystyle (-cos(3x))/(3) + C`