Final answer:
A. The potential energy at point A is 102900J.
B. The velocity at the top of the loop is 24.19 m/s.
Step-by-step explanation:
A. Calculate the potential energy at point A.
The potential energy at point A can be calculated using the formula
PE=mgh, where: m is the mass of the roller coaster (350 kg), g is the acceleration due to gravity (approximately 9.8m/s2), and h is the height of point A above the reference point. Given that the roller coaster starts from rest, the initial kinetic energy is zero. Therefore, all the initial energy is in the form of potential energy.
Let's assume the height of point A above the reference point is 30m (you need to use the actual height from the problem statement for a precise calculation):
PE_A = mgh
PE_A = (350kg) x (30m)
PE_A = 102900J
Therefore, the potential energy at point A is 102900J.
B. Determine the velocity at the top of the loop.
v_top =
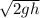
The velocity at the top of the loop can be determined using the conservation of energy. At the top, the potential energy is converted into kinetic energy. The kinetic energy is given by KE= 1/2 mv²
Setting the potential energy at point A equal to the kinetic energy at the top:
mgh = 1/2 mv²_top
Solving for v_top:
v_top =
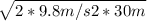
v_top = 24.19 m/s
Therefore, the velocity at the top of the loop is 24.19 m/s.
C. Analyze the forces acting on the roller coaster at different points.
The forces acting on the roller coaster include:
Gravity (F_gravity): This force acts vertically downward and is responsible for the potential energy and acceleration of the coaster.
Normal Force (F_normal): This force acts perpendicular to the surface of the track and prevents the roller coaster from falling through the track.
Centripetal Force (F_centripetal): This force acts toward the center of the circular loop and is responsible for keeping the coaster in circular motion at the top of the loop.
At point A, F_gravity is the only force acting on the coaster.
At the top of the loop, F_gravity & F_normal both contribute to the centripetal force required to keep the coaster on the circular path.
D. Discuss the conditions required for the coaster to remain on the track.
For the coaster to remain on the track:
The sum of the forces in the vertical direction (up and down) must be balanced to prevent vertical motion (falling through the track).
The centripetal force must be sufficient to keep the coaster moving in a circular path. This requires a minimum velocity at the top of the loop, and it depends on the radius of the loop and the gravitational acceleration.
Friction between the coaster wheels and the track should be negligible or considered in the analysis. In this case, it's stated that the track is frictionless, which simplifies the analysis.
These conditions ensure that the coaster stays on the track and completes the loop-the-loop without derailing or losing contact with the track.