1. The volume of the solid formed by rotating the region enclosed by
 about the x-axis is approximately
about the x-axis is approximately

2. The volume of the solid obtained by rotating the region bounded by
 about the x-axis is
about the x-axis is
 .
.
3. For the solid formed by rotating the region bounded by
 and
and
 about the x-axis, the volume depends on the upper limit of integration
about the x-axis, the volume depends on the upper limit of integration
 .
.
Question 1:
To find the volume of the solid formed by rotating the region enclosed by
 about the x-axis, we can use the disk method. The volume
about the x-axis, we can use the disk method. The volume
 is given by:
is given by:
![\[V = \pi \int_(0)^(0.9) (e^(2x) + 3)^2 \,dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k8vjzonq7r2rcxe7w2cp73izhy6a8ift54.png)
Now, integrate with respect to \(x\):
![\[V = \pi \int_(0)^(0.9) (e^(4x) + 6e^(2x) + 9) \,dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1ei9tdglmajmx710lgq5q8pfu976yp4b0w.png)
![\[V = \pi \left[(1)/(4)e^(4x) + 3e^(2x) + 9x\right]_(0)^(0.9)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yxp2a2h6gl8qwxbi5148pt7yh6o44fy0rw.png)
![\[V = \pi \left[(1)/(4)e^(3.6) + 3e^(1.8) + 9(0.9)\right]\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v5cv0z9lagpyuqj5gtezfdtbou07uida3c.png)
![\[V \approx 51.67 \pi\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9kfkm2txzhrngvs8mkrnj2nn3my6lazumf.png)
Therefore, the volume of the solid formed by rotating the region about the x-axis is approximately
 .
.
Question 2:
To find the volume of the solid obtained by rotating the region bounded by
 , and
, and
 about the x-axis, we again use the disk method. The volume
about the x-axis, we again use the disk method. The volume
 is given by:
is given by:
![\[V = \pi \int_(3)^(9) \left((1)/(√(x+3))\right)^2 \,dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hw0xddckksnfyubk0qqkh3845le076ixfd.png)
Now, integrate with respect to
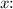
![\[V = \pi \int_(3)^(9) (1)/(x+3) \,dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xt3o0ugp01zzbhu8shnd8zz83yy0ig377j.png)
![\[V = \pi \ln|x+3| \Big|_(3)^(9)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p8sc8khnlu35p94awuauvcb15uhyz3ldhh.png)
![\[V = \pi (\ln 12 - \ln 6)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zxleq12n6966g9pk431s45926glmxgsv05.png)
![\[V = \pi \ln 2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1qgrd3wrzadc8eaxykfouxtgkgz0xevkom.png)
The volume of the solid formed by rotating the region about the x-axis is
 .
.
Question 3:
The solid formed by rotating the region bounded by
 about the x-axis can be calculated using the disk method:
about the x-axis can be calculated using the disk method:
![\[V = \pi \int_(0.5)^(b) (e^(3x) + 3)^2 \,dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dcsj38ataxbr0dndsu4n2x79o3keefswm8.png)
After integrating and evaluating, the volume
 can be expressed in terms of
can be expressed in terms of
 .
.
The volume of the solid formed by rotating the region about the x-axis depends on the upper limit of integration
 .
.
The question probable maybe:
1. Find the volume of the solid formed by rotating the region enclosed by y=e^2x +3, y=0, x=0, x=0.9 about the x-axis. Volume:____
2. Find the volume of the solid obtained by rotating the region bounded by y=1/√ (x+3), x=3, x=9, and y=0, about the x-axis. Volume:____
3. A solid is formed by rotating the region in the first quadrant of the xy-plane bounded by the graphs of y=e^3x+3 and x=0.5 about the x-axis. Volume:____