Question

Write the point-slope form of the equation of the line that passes through the points (-8, 2) and (1, -4). Include your work in your final answer. Type your answer in the box provided to submit your solution.

Answer 1

`\displaystyle (y - 2) = -(2)/(3)\, (x + 8)`.

Explanation:

Given two points
`(x_0,\, y_0)` and
`(x_1,\, y_1)` on a line in
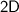`\mathsf{2D}`, the slope of that line would be:

`\begin{aligned} m &= (y_1 - y_0)/(x_1 - x_0) \\ &= (-4 - 2)/(1 - (-8)) = -(2)/(3)\end{aligned}`.

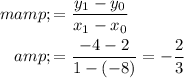For a line with slope
`m` and a point
`(x_0,\, y_0)`, the point-slope equation of that line would be:

`y - y_0 = m \, (x - x_0)`.

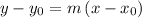It was already found that for this line, slope
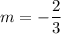`\displaystyle m = -(2)/(3)`. Take
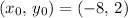`(x_0,\, y_0) = (-8,\, 2)`. That is:
`x_0 = -8` and
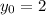`y_0 = 2`. Find the equation of this line in point-slope form:

`\displaystyle (y - \underbrace{2}_(y_0)) = \underbrace{\left(-(2)/(3)\right)}_(m)\, (x - \underbrace{(-8)}_(x_0))`.

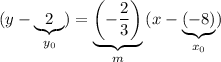Equivalently:

`\displaystyle (y - 2) = -(2)/(3)\, (x + 8)`.