Explanation:
1. First things first, the binomial tells us the zeroes.
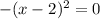
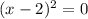
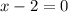
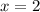
This root has a multiplicity of 2, so this root will "bounces off the x axis"

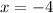
Our x intercepts are
2 and -4
This root has a multiplicty of 1, so it will cross thorough the x axis.
Our leading degree is odd and we have a negative leading coefficient so
as x approaches ♾️, f(x) approaches negative ♾️
and as x approaches negative ♾️, f(x) approaches ♾️.
Our y intercept can be found by letting x=0,
so

So our y intercept is -16.
For Rational Functions, if the numerator and denominator share the same factor they are considered a removable discontinuity or hole.
Set it equal to 0.
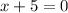

So we have a hole at x=-5.
Next, simplify the fraction.
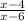
Now, plug in -5
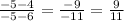
So we have a hole at (-5,9/11).
To find y intercept, let x=0,
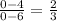
To find Vertical Asymptote, set denominator equal to 0
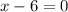

Draw a vertical dotted line at x=6
To find HA, this is the only case since the numerator and denominator has the same degree.
So using the leading coefficients, divide the numerator leading coefficient/ denominator leading coefficient.
The leading coefficient for both is 1 so
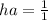
So our HA is y=1.
Draw a horizon tal dotted line at y=1
We have no slope asymptote.
The graph is above.
Part 3:
(3x-1)(2x+1)>0
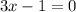
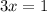
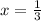
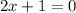


We have three possible regions, when x is positive
- When x is less than -1/2
- When x lies between -1/2 and 1/3
- When x is greater than 1/3
Pick a random number less than -1/2 and plug it in the inequality to see if it true.
Let use -1
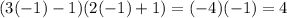
Since 4>0, Whenever x is less than -1/2, the function is positive (greater than zero)
Let's try the next region.
Let use 0

So this solution won't work
Let try the next region, let use 1.
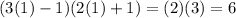
Since 6>0, Whenever x is greater than 1/3, the function is positive(greater than zero).
Our answer is
(-oo,-1/2) U (1/3,oo).
Part 4:
We know x cannot be -2 because
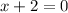

So -2 can not be in our answer.
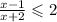
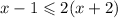
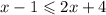
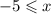
So
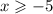
However x can not be -2. so we say
[-5,-2) U (-2,oo)