Answer:
$3.80 = cost of one gallon of milk.
$1.60 = cost of one bottle of water.
$0.80 = cost of one snack-size bag of chips.
Explanation:
Define the variables:
- Let x = one gallon of milk.
- Let y = one bottle of water.
- Let z = one snack-size bag of chips.
Total items purchased:
- 3 gallons of milk.
- 4 bottles of water.
- 7 snack-size bags of chips.
Given information:
- Total bill (before tax) = $23.40.
- A bottle of water costs twice as much as a bag of chips.
- A gallon of milk costs $2.20 more than a bottle of water.
Create a system of equations with the given information:
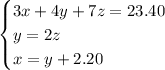
Rearrange the second equation to make z the subject:
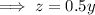
Substitute the found expression for z and the third equation into the first equation and solve for y:
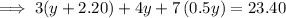
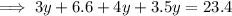

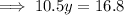
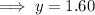
Substitute the found value of y into the third equation and solve for x:
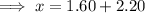
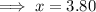
Substitute the found value of y into the second equation and solve for z:
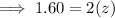

Conclusion:
- $3.80 = cost of one gallon of milk.
- $1.60 = cost of one bottle of water.
- $0.80 = cost of one snack-size bag of chips.