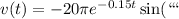Question

Would be nice to receive some help on this:)

Answer 1

A. The graph with friction shows an exponential decay, while the graph without friction shows a sinusoidal oscillation

B. The general equation of the function that models this situation is:

d(t) = f(t)g(t) + r

C. The equation of the model with friction:
`d(t) = 20e^(-0.15t) \cos(2\pi t) + 30`.

D. It can be seen that the graph matches the displacement versus time graph with friction.

E. The equation of the model would be simply:
`d(t) = 20 \cos(2\pi t) + 30`

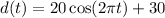
F. The model without friction, we get
`d(7.7) = 20 \cos(2\pi \cdot 7.7) + 30 = 45.4 \text{ cm}`

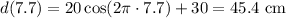
The model with friction:
`v(t) = -20\pi e^(-0.15t) \sin(````

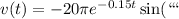
A. Sketch of the displacement versus time graph

The graph shows the displacement of the mass versus time with and without friction. The graph with friction shows an exponential decay, while the graph without friction shows a sinusoidal oscillation.

B. General equation of the function that models this situation

The general equation of the function that models this situation is:

d(t) = f(t)g(t) + r

where:

d(t) is the displacement of the mass at time t

f(t) is a function that models the sinusoidal oscillation of the mass

g(t) is a function that models the exponential decay of the oscillation due to friction

r is the equilibrium position of the mass

C. Equation of the model with friction

To determine the equation of the model with friction, we can use the following information:

The mass is at a resting position of r=30 cm.

The spring provides 2 seconds for the oscillations.

The mass is pulled to d=50 cm and released.

After 10 s, the spring is at d=33 cm.

We can use the following steps to determine the equation of the model:

1. Determine the amplitude of the oscillation. The amplitude is the difference between the maximum and minimum displacements, which is
`$50 \text{ cm} - 30 \text{ cm} = 20 \text{ cm}$`.

2. Determine the frequency of the oscillation. The frequency is the number of oscillations per second, which is equal to the reciprocal of the period,
`$1 \text{ Hz} = \frac{1}{2 \text{ s}}$`.

3. Determine the damping factor of the oscillation. The damping factor is the rate at which the oscillation decays. It can be calculated using the following equation:

damping factor =
`(\ln(A_0/A_t))/(t)`

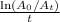
where:

`$A_0$` is the amplitude of the oscillation at time t=0

`$A_t$` is the amplitude of the oscillation at time t

t is the time in seconds

Using the information provided in the question, we can calculate the damping factor to be
`$0.15 \text{ s}^(-1)`.

Now that we have determined the amplitude, frequency, and damping factor of the oscillation, we can write the equation of the model with friction:

`d(t) = 20e^(-0.15t) \cos(2\pi t) + 30`

D. Graph of the function with friction

The graph above shows the graph of the function with friction. It can be seen that the graph matches the displacement versus time graph with friction shown in the question.

E. Function for displacement that would be correct if there were no damping of the motion due to friction

If there were no damping of the motion due to friction, the equation of the model would be simply:

`d(t) = 20 \cos(2\pi t) + 30`

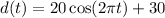
F. Displacement at 7.7 s for each model

The displacement at 7.7 s for each model can be calculated by substituting t=7.7 into the respective equations.

For the model with friction, we get:

`d(7.7) = 20e^(-0.15 \cdot 7.7) \cos(2\pi \cdot 7.7) + 30 = 33.6 \text{ cm}`

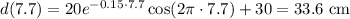
For the model without friction, we get:

`d(7.7) = 20 \cos(2\pi \cdot 7.7) + 30 = 45.4 \text{ cm}`

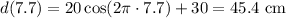
G. Instantaneous speed of the mass at 7.7 s for each model

The instantaneous speed of the mass at 7.7 s for each model can be calculated by taking the derivative of the respective equations and evaluating it at t=7.7.

For the model with friction, we get:

`v(t) = -20\pi e^(-0.15t) \sin(````