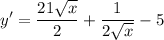Question

Y=sqrt(x)+7x(3/2)-5x+12

Answer 1

Explanation:

This is the answer thank you :)

Answer 2

`\displaystyle y' = (21√(x))/(2) + (1)/(2√(x)) - 5`

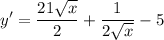
General Formulas and Concepts:

Algebra I

• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`

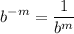
Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

`\displaystyle y = √(x) + 7x^{(3)/(2)} - 5x + 12`

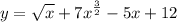
Step 2: Differentiate

1. Rewrite:
   `\displaystyle y' = x^{(1)/(2)} + 7x^{(3)/(2)} - 5x + 12`
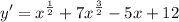
2. Basic Power Rule:
   `\displaystyle y' = (1)/(2)x^{(1)/(2) - 1} + (3)/(2) \cdot 7x^{(3)/(2) - 1} - 1 \cdot 5x^(1 - 1)`
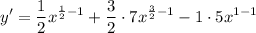
3. Simplify:
   `\displaystyle y' = (1)/(2)x^{(-1)/(2)} + \frac{21x^{(1)/(2)}}{2} - 5`
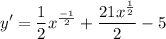
4. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle y' = \frac{1}{2x^{(1)/(2)}} + \frac{21x^{(1)/(2)}}{2} - 5`
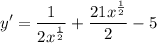
5. Rewrite:
   `\displaystyle y' = (1)/(2√(x)) + (21√(x))/(2) - 5`
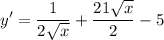
6. Rearrange:
   `\displaystyle y' = (21√(x))/(2) + (1)/(2√(x)) - 5`