Question

f(t) = 3δ(t) tu(t) (b) f(t) = (t − 2)u(t − 2) (c) f(t) = tu(t − 2) (d) f(t) = e −3(t−1)u(t − 1) (e) f(t) = e −3tu(t − 1)

Answer 1

(a)
`\( f(t) = 3\delta(t) \cdot u(t) \`): Represents a function with a magnitude of 3 at t = 0 multiplied by the unit step function for t ≥ 0.

(b) f(t) = (t - 2)u(t - 2): Starts at t = 2, growing linearly from that point due to the unit step function for t ≥ 2.

(c) f(t) = t ·u(t - 2): Begins at t = 2 with linear growth from that time onward because of the unit step function.

(d)
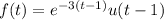`\( f(t) = e^(-3(t-1))u(t - 1) \)`: Depicts an exponentially decaying function starting at t = 1 enforced by the unit step function for t ≥ 1.

(e)
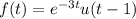`\( f(t) = e^(-3t)u(t - 1) \)`: Represents an exponentially decaying function starting at t = 0 due to u(t - 1) for t ≥ 1 .

Step-by-step explanation:

(a)
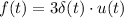`\( f(t) = 3\delta(t) \cdot u(t) \)`combines the delta function
`\( \delta(t) \)` with the unit step function u(t). The delta function is non-zero only at t = 0 and has a magnitude of 1, amplified by 3 in this case, and the unit step function u(t) ensures the function exists for t ≥0.

(b) f(t) = (t - 2)u(t - 2) signifies a function that starts at t = 2, where the unit step function u(t - 2) becomes active, allowing the function to exist and grow linearly for t ≥2.

(c) f(t) = t·u(t - 2) denotes a function that commences at t = 2 due to u(t - 2), starting with a linear increase from that point onward.

(d)
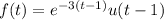`\( f(t) = e^(-3(t-1))u(t - 1) \)` represents an exponential decay function that initiates at t = 1 thanks to the unit step function u(t - 1), ensuring the function's existence for t ≥1.

(e)
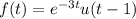`\( f(t) = e^(-3t)u(t - 1) \)`represents an exponential decay function that starts at t = 0, controlled by the unit step function u(t - 1) , which ensures the function exists for t ≥ 1 .

Question:

Consider the following functions of time, f(t), within the domain of real numbers t :

(a)
`\( f(t) = 3\delta(t) \cdot u(t) \)`

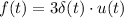
(b) f(t) = (t - 2)u(t - 2)

(c) f(t) = t · u(t - 2)

(d)
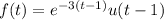
`\( f(t) = e^(-3(t-1))u(t - 1) \)`

(e)
`\( f(t) = e^(-3t)u(t - 1) \)`

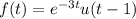
Analyze and describe each function in terms of its properties, behavior, and mathematical representations within the context of time t and the unit step function u(t).