Question

Does anyone know the answer to this simple geometry?

Answer 1

Step-by-step explanation: Let x = 2, y = 5 and z=?

Here z is the unknown length.

here z is 4.6

Answer 2

4.6

Explanation:

we can use the Pythagorean theorem of

A^2 + B^2 = C^2

where A and B are the (lengths of) short sides of a right triangle and C is the (length of) long side.

Here, we have an unknown side, let's call it X, and we know that:

2^2 + X^2 = 5^2

So

4 + X^2 = 25

X^2 = 25 - 4 = 21

X^2 = 21

X =
`√(21)`

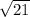
Let's find the root of 21 rounded to the nearest tenth (or you can probably use a calculator, the method I show below is mathematically proper but not part of the curriculum).

the root of 21 is bigger than the root of 16 but smaller than the root of 25. So the number we're looking for is between 4 and 5.

21 is pretty much in the middle, so let's start by checking if it's bigger than 4.5

4.5^2 = 20.25

So 4.5 is a bit too small

Let's check 4.6

4.6^2 = 21.16

So 4.6 is a bit too big.

So we know our number is between 4.5 and 4.6 now. To have a good rounding to the nearest tenth, we only need to find out if it's over or below 4.55 (as this gives us direct rounding to the nearest tenth).

4.55^2 = 20.7025

So X is bigger than 4.55 and smaller than 4.6, hence the answer rounded to the nearest tenth is 4.6