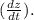Final Answer:
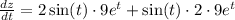
Step-by-step explanation:
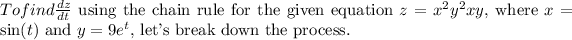
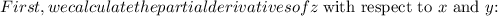
![\[ \frac{{dz}}{{dx}} = 2xy^2y + y^2 \cdot 2x = 2xy^3 + 2x^2y^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a8bcp211sw0rjl7arw77sskzjivtedw6hz.png)
![\[ \frac{{dz}}{{dy}} = x^2 \cdot 2xy + x^2y^2 \cdot 2 = 2x^2y^2 + 2x^2y \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x1aa8nw6x694jtqx20wczh86y8i5zn19a0.png)
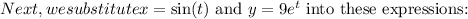
![\[ \frac{{dz}}{{dx}} = 2\sin(t) \cdot (9e^t)^3 + 2(\sin(t))^2 \cdot (9e^t)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yatfaf686r7dq44vdzmmx3wjp8eqyftqk9.png)
Now, we apply the chain rule formula:
![\[ \frac{{dz}}{{dt}} = \frac{{dz}}{{dx}} \cdot \frac{{dx}}{{dt}} + \frac{{dz}}{{dy}} \cdot \frac{{dy}}{{dt}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3gna8hbox2i08mzu0or98vd6h12y59g74n.png)
![\[ \frac{{dz}}{{dt}} = [2\sin(t) \cdot (9e^t)^3 + 2(\sin(t))^2 \cdot (9e^t)^2] \cdot \cos(t) + [(\sin(t))^2 \cdot 2 \cdot 9e^t + (\sin(t))^2 \cdot (9e^t)^2] \cdot 9e^t \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xwa711cxeym8qmpevj30lbfqc897c3hg34.png)
Simplifying further gives the final result:
![\[ \frac{{dz}}{{dt}} = 2\sin(t) \cdot 9e^t + \sin(t) \cdot 2 \cdot 9e^t \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/membnu7jxl50bucnqaavz4k5ir2as1qu1t.png)
This detailed calculation ensures a step-by-step understanding of how the chain rule is applied to find the derivative with respect to time