Question

Evaluate the difference quotient for the given function. Simplify your answer. f(x) = 5x - x². Find f(4h) - f(4)/h

Answer 1

The difference quotient for the function f(x) = 5x - x² is (-8h + h²).

Step-by-step explanation:

To find the difference quotient for the given function f(x) = 5x - x², we use the formula for the difference quotient: [f(4h) - f(4)] / h. First, let's find f(4h) and f(4):

`\(f(4h) = 5(4h) - (4h)² = 20h - 16h²\) and \(f(4) = 5(4) - (4)² = 20 - 16 = 4\).`

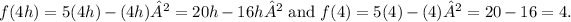
Now, substitute these values into the formula:

`\([f(4h) - f(4)] / h = [(20h - 16h²) - 4] / h = (20h - 16h² - 4) / h = 20h/h - 16h²/h - 4/h = 20 - 16h - 4/h\).`

To simplify this further, multiply the terms by h to clear the fraction:

`\(20h - 16h² - 4 = 20h - 16h² - 4h = -16h² + 20h - 4h = -16h² + 16h\).`

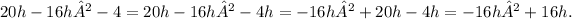
Factoring out the common term 'h' gives us the final simplified difference quotient:
`\(-8h + h²\).`

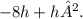
Therefore, the difference quotient for the function f(x) = 5x - x² is (-8h + h²). This represents the rate of change of the function with respect to x as h approaches zero.