Question

Please helppppp!!!!!!

Answer 1

To show that x + 5 is a factor of
`f(x) = x^4 + 5x^3 - 27x - 135`, we use the Remainder Theorem by substituting x = -5 into the function, yielding 0; thus, confirming that x + 5 is a factor. Further factoring would involve dividing f(x) by x + 5 to get a cubic polynomial and then factoring that polynomial.

To show that x + 5 is a factor of
`f(x) = x^4 + 5x^3 - 27x - 135`, we perform polynomial division or apply the Remainder Theorem. Using the Remainder Theorem, we substitute x = -5 into the function:

`f(-5) = (-5)^4 + 5(-5)^3 - 27(-5) - 135`

`= 625 - 625 + 135 - 135 = 0.`

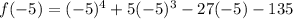
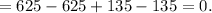
Since f(-5) = 0, x + 5 is indeed a factor of f(x). Now, let's factor the function completely. We can start by using synthetic division or long division to divide f(x) by x + 5, which will give us a cubic polynomial. After finding the cubic polynomial, we can factor it further, possibly factoring by grouping or finding other roots using techniques such as the Rational Root Theorem.