Question

if you invest $20,000 in an actively managed mutual fund that charges a 2 nnual fee, you will pay $400 annual fees but only if the value of the fund increases.

Answer 1

Using the compound interest formula, Alexx, who invested directly and earned a higher interest rate, will have $821.33 more than Spenser after 30 years because Spenser's investment through a retirement fund incurred an administrative fee which reduced his annual return.

Step-by-step explanation:

The question involves calculating the future value of investments considering different annual rates of return and fees, which falls into the subject of Mathematics and is typically encountered at the High School grade level.

To compare the amount between Alexx's and Spenser's investments over 30 years, we must apply the formula for compound interest,
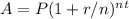`A = P(1 + r/n)^n^t`, where A is the future value of the investment, P is the principal amount, r is the annual interest rate, n is the number of times that interest is compounded per year, and t is the time the money is invested for in years.

Alexx invests $5,000 directly and earns 5% a year. Using the compound interest formula, Alexx's investment after 30 years will be:

5,000(1 + 0.05)30 = $21,610.35

Spenser uses a retirement fund and, after the 0.25% fee, earns 4.75% a year.

Using the compound interest formula, Spenser's investment after 30 years will be:

5,000(1 + 0.0475)30 = $20,789.02

The difference between Alexx and Spenser's investments after 30 years is:

$21,610.35 - $20,789.02 = $821.33

Therefore, Alexx will have $821.33 more than Spenser after 30 years due to the higher interest rate he earned by investing directly without the retirement fund's administrative fee.