Question

Use Lagrange multipliers to find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the given plane. What is the volume of the rectangular box?

Answer 1

The volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the given plane is
`\( (8)/(3) \)` cubic units.

Step-by-step explanation:

To find the maximum volume of the rectangular box, we'll utilize Lagrange multipliers. Let
`\( x, y, z \)` represent the lengths of the sides of the box, with one vertex on the plane
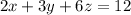`\( 2x + 3y + 6z = 12 \)`. The objective function to maximize is the volume,
`\( V = xyz \)`, subject to the constraint
`\( g(x, y, z) = 2x + 3y + 6z - 12 = 0 \).`

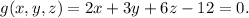
Setting up the Lagrangian:

`\[ L(x, y, z, \lambda) = xyz - \lambda(2x + 3y + 6z - 12) \]`

Taking partial derivatives with respect to
`\( x, y, z, \)`and
`\( \lambda \)` and setting them to zero:

`\[ (\partial L)/(\partial x) = yz - 2\lambda = 0 \]`

`\[ (\partial L)/(\partial y) = xz - 3\lambda = 0 \]`

`\[ (\partial L)/(\partial z) = xy - 6\lambda = 0 \]`

`\[ (\partial L)/(\partial \lambda) = 2x + 3y + 6z - 12 = 0 \]`

Solving these equations simultaneously gives us
`\( x = (4)/(3), y = (2)/(3), z = 1 \)`. Substituting these values into the volume equation
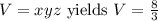`\( V = xyz \) yields \( V = (8)/(3) \)` cubic units.

The critical point
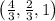`\( \left((4)/(3), (2)/(3), 1\right) \)` corresponds to the maximum volume of the rectangular box in the first octant with the specified constraints. Hence, the maximum volume of the box is
`\( (8)/(3) \)` cubic units.