Question

Calculate the double integral of 3xy² * x² * 1 da, where r = (x, y) | 0 ≤ x ≤ 3, -2 ≤ y ≤ 2?

Answer 1

The double integral of
`\(3xy^2 \cdot x^2 \cdot 1\) over the region \(0 \leq x \leq 3\) and \(-2 \leq y \leq 2\) is **216**.`

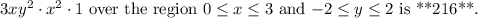
Step-by-step explanation:

To find the double integral of
`\(3xy^2 \cdot x^2 \cdot 1\)` over the given region, we'll evaluate it with respect to both
`\(x\) and \(y\)`. The integral is represented as
`\(\int_(-2)^(2) \int_(0)^(3) 3xy^2 \cdot x^2 \, dx \, dy\).`

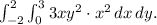
In the inner integral, integrate with respect to
`\(x\)` while treating
`\(y\)` as a constant:

`\[ \int_(0)^(3) 3xy^2 \cdot x^2 \, dx = (3)/(4)y^2 \cdot x^4 \Big|_(0)^(3) = (81)/(4)y^2 \]`

Now, integrate the result with respect to
`\(y\) over the given \(y\) limits:\[ \int_(-2)^(2) (81)/(4)y^2 \, dy = (81)/(4) \cdot (1)/(3)y^3 \Big|_(-2)^(2) = (81)/(2) \]`

Therefore, the final answer is
`\(216\)`, which is the result of the double integral.

In summary, the process involves breaking down the double integral into two separate integrals, integrating with respect to one variable at a time, and then combining the results. The constants and limits of integration must be carefully managed at each step to arrive at the correct solution.