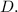Final Answer
If
 is analytic in a domain
is analytic in a domain
 , and if
, and if
 is constant, then
is constant, then
 is a constant function.
is a constant function.
Step-by-step explanation:
Analytic functions are complex functions that can be represented by power series expansions. When
 is constant, it implies that the modulus (magnitude) of
is constant, it implies that the modulus (magnitude) of
 is constant throughout the domain
is constant throughout the domain
 . To understand why
. To understand why
 must be a constant function, we can use the Cauchy-Riemann equations.
must be a constant function, we can use the Cauchy-Riemann equations.
The Cauchy-Riemann equations state that if
 is analytic, where
is analytic, where
 and
and
 are real-valued functions of
are real-valued functions of
 and
and
 (the real and imaginary parts of
(the real and imaginary parts of
 , then the partial derivatives of
, then the partial derivatives of
 and
and
 satisfy specific relationships. In particular, if
satisfy specific relationships. In particular, if
 is constant, then the modulus of
is constant, then the modulus of
 is constant, and this implies that
is constant, and this implies that
 and
and
 satisfy the conditions:
satisfy the conditions:
![\[ (\partial u)/(\partial x) = (\partial v)/(\partial y) \quad \text{and} \quad (\partial u)/(\partial y) = -(\partial v)/(\partial x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b1vvjzi9bkfptrd183dq0syb9aq2xas7yb.png)
When
 is constant, the magnitude of
is constant, the magnitude of
 does not vary with respect to
does not vary with respect to
 and
and
 , which implies that both
, which implies that both
 ) and
) and
 are zero. Similarly,
are zero. Similarly,
 and
and
 are also zero. These conditions, combined with the Cauchy-Riemann equations, lead to
are also zero. These conditions, combined with the Cauchy-Riemann equations, lead to
 , indicating that
, indicating that
 and
and
 are constant. Consequently,
are constant. Consequently,
 is a constant function in the given domain
is a constant function in the given domain