Question

Use the given information to find f '(2).

Answer 1

The derivative of f(x) = 3x² - 2x + 1 is (f'(x) = 6x - 2), and when (x = 2), (f'(2) = 10).

Step-by-step explanation:

To find the derivative f'(x) of (f(x) = 3x² - 2x + 1), apply the power rule for derivatives. The derivative of 3x² is 6x, and the derivative of -2x is (-2). The constant term (1) differentiates to (0) as it vanishes when finding the derivative of a constant. Therefore, (f'(x) = 6x - 2).

Substituting (x = 2) into the derivative f'(x) gives f'(2) = 6(2) - 2 = 12 - 2 = 10. Thus, the value of the derivative f'(x) at (x = 2) is 10.

Here is complete question;

"Given the function f(x) = 3x² - 2x + 1, find the derivative f'(x) and then evaluate f'(2). Show the steps involved in finding the derivative and the numerical calculation of f'(2)."

Answer 2

The final answer for
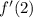`\(f'(2)\)` is 16, indicating that at (x = 2), the rate of change of the function
`\(f(x)\)` is 16.

Step-by-step explanation:

The derivative of the quotient of two functions, \( f(x) = \frac{g(x)}{h(x)} \), is given by the formula:

`\[ f'(x) = (g'(x)h(x) - g(x)h'(x))/((h(x))^2) \]`

Given the values for
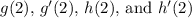`\( g(2) \), \( g'(2) \), \( h(2) \), and \( h'(2) \)`, we can plug these into the formula to find ( f'(2) ):

`\[ f'(2) = (g'(2)h(2) - g(2)h'(2))/((h(2))^2) \]`

Substitute the provided values:

`\[ f'(2) = ((-4)(-1) - (4)(3))/((-1)^2) \]`

`\[ f'(2) = (4 + 12)/(1) \]`

`\[ f'(2) = (16)/(1) \]`

`\[ f'(2) = 16 \]`

Therefore, ( f'(2) = 16 ).

In summary, the derivative of the given function at ( x = 2 ) is ( 16 ). This means that at the point ( x = 2 ), the rate of change of the function ( f(x) ) is 16.

Complete Question:
Use the given information to find f '(2).

g(2) = 4 and g'(2) = −4

h(2) = −1 and h'(2) = 3

f(x) =

g(x)

h(x)

f '(2)=