Final Answer:
The given limit expression can be simplified to

Step-by-step explanation:
We are given tha
![t \( g(7) = 2 \) and \( \lim_{{x \to 7}} [3f(x)f(x)g(x)] = 25 \).](https://img.qammunity.org/2024/formulas/mathematics/high-school/bpcwt0jsr328tkq9o2u3sjhjhm44k43qeb.png) We need to find
We need to find
 . The given limit can be expressed as
. The given limit can be expressed as
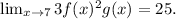
Since
![\( \lim_{{x \to c}} g(x) = g(c) \) when \( g(x) \) is continuous at \( x = c \), we can substitute \( g(7) = 2 \) into the limit expression:\[ \lim_{{x \to 7}} 3f(x)^2 \cdot 2 = 25 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qxe9l1mc3ei6sz3zcex65gx0a88kx6jf49.png)
Solving for
![\( \lim_{{x \to 7}} 3f(x)^2 = (25)/(2) \). Now, we know \( \lim_{{x \to c}} f(x)^2 = [f(c)]^2 \) when \( f(x) \) is continuous at \( x = c \). So,\[ 3[f(7)]^2 = (25)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/70y1btdwlnz6vkyeu6ez7cdgb78c90b0ss.png)
Solving for
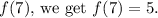
In summary, by using the properties of limits and continuity, we found that \
 is the solution to the given problem.
is the solution to the given problem.