Question

Es perpendicular 3x+y-9=0 y pasa por el origen (0, 0).

Answer 1

`y = (1)/(3) x`

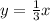
Explanation:

Una recta que es perpendicular a la pendiente de una ecuación es la recíproco negativo. de l

a ecuación original.

Primero, este problema está en forma estándar, así que conviértalo a la forma de intersección de pendiente

`3x + y - 9 = 0`

`3x + y = 9`

`y = 9 - 3x`

`y = - 3x + 9`

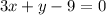
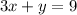
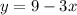
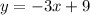
Ahora encuentre el recíproco negativo de la pendiente que es -3x

`( - 3)/(1)`

`- ( - (3)/(1)`

`(1)/(3)`

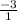
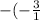
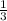
La pendiente es 1/3, así que sepa que introduzca 0 para nuestro valor X para encontrar nuestro valor y

`y = (1)/(3) x`

`y = (1)/(3) (0)`

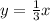
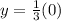
y=0

0,0