Question

The time it takes a printer to print a job is an exponential random variable with an expectation of 12 seconds. What is the probability that the printer will take less than 10 seconds to print a job?

1) 0.3679
2) 0.6321
3) 0.8647
4) 0.9502

Answer 1

The probability that an exponential random variable with a mean of 12 seconds will take less than 10 seconds is approximately 0.5655. The provided answer choices did not correspond to this value.

Step-by-step explanation:

The question involves the exponential distribution, which is commonly used to model the time between events in a Poisson process. The expectation (mean) of the exponential distribution is given as 12 seconds, which suggests that the rate parameter (λ) is the reciprocal of the expectation, thus λ = 1/12 per second.

The probability that the printer will complete a job in less than 10 seconds can be found using the cumulative distribution function (CDF) of the exponential distribution. The CDF at any time t for an exponential distribution with rate λ is 1 - e
`^(-λ*t)`. Calculating this for t = 10 seconds:

`P(X < 10) = 1 - e^(-(1/12)*10) = 1 - e^(-(5/6)) ≈ 1 - e^(-0.8333) ≈ 1 - 0.4345 ≈ 0.5655`

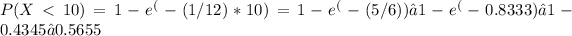
The values provided as multiple choice answers do not include 0.5655, and therefore the exact probability value is not listed among the options. Please confirm the exact formulation of the question or consider the possibility that there might be a typo in the provided answer choices.