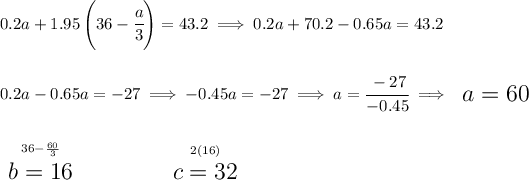Question

A chemist has three different acid solutions. The first acid solution contains

20% acid, the second contains 35% and the third contains 80% . They want to use all three solutions to obtain a mixture of 108 liters containing 40% acid, using 2 times as much of the 80% solution as the 35% solution. How many liters of each solution should be used?

Answer 1

a = solution at 20% acid

b = solution at 35% acid

c = solution at 80% acid

now, we know she wants to use two times as much of "c" as there's of "b", which is a mumble jumble for saying whatever "b" is, well "c" is twice that much, namely c = 2b. We also know the whole mixture will be 108 liters of 40% acid.

let's convert those percentages to decimals and let's see how much all those liters are

`\begin{array}{lcccl} &\stackrel{liters}{quantity}&\stackrel{\textit{\% of }}{amount}&\stackrel{\textit{liters of }}{amount}\\ \cline{2-4}&\\ \textit{20\% sol'n}&a&0.20&0.2a\\ \textit{35\% sol'n}&b&0.35&0.35b\\ \boxed{\textit{80\% sol'n}}&c&0.80&0.8c\\ \textit{80\% sol'n}&2b&0.80&1.6b\\ \cline{2-4}&\\ mixture&108&0.40&43.2 \end{array}~\hfill \begin{cases} a+b+\stackrel{c}{2b}=108\\\\ 0.2a+0.35b+1.6b=43.2 \end{cases} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{using the 1st equation}}{a+b+2b=108\implies} a+3b=108\implies 3b=108-a \\\\\\ b=\cfrac{108-a}{3}\implies \boxed{b=36-\cfrac{a}{3}} \\\\\\ \stackrel{\textit{substituting on the 2nd equation}}{0.2a+0.35b+1.6b=43.2}\implies 0.2a+1.95b=43.2`

`0.2a+1.95\left( 36-\cfrac{a}{3} \right)=43.2\implies 0.2a+70.2-0.65a=43.2 \\\\\\ 0.2a-0.65a=-27\implies -0.45a=-27\implies a=\cfrac{-27}{-0.45}\implies {\Large \begin{array}{llll} a=60 \end{array}} \\\\\\ \stackrel{36-(60)/(3)}{{\Large \begin{array}{llll} b=16 \end{array}}} \hspace{5em} \stackrel{2(16)}{{\Large \begin{array}{llll} c=32 \end{array}}}`