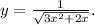Final Answer:
The solution to the given initial-value problem,
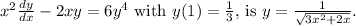
Step-by-step explanation:
To solve this Bernoulli equation, we'll first transform it to a linear differential equation through substitution. Let
 . Rearranging the original equation in terms of
. Rearranging the original equation in terms of
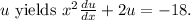
This is now a linear first-order differential equation, solvable using an integrating factor
 Multiplying both sides of the equation by
Multiplying both sides of the equation by
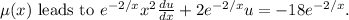
Recognizing the left-hand side as the derivative of
 with respect to x, we integrate both sides to get
with respect to x, we integrate both sides to get
 Solving the integral and substituting
Solving the integral and substituting
![\(u = y^(-3)\) yields \(y = \frac{1}{\sqrt[3]{C - 18\left(-(x)/(2)\right)e^(2/x)}} = (1)/(√(3x^2 + 2x))\).](https://img.qammunity.org/2024/formulas/mathematics/high-school/axuhc02nou2juuqzlmdv5zb3sdn0x05pmh.png)
Applying the initial condition
 allows us to determine the value of
allows us to determine the value of
 and results in the final solution
and results in the final solution