Question

A spring with mass is free to move in how many dimensions?

1) 1
2) 2
3) 3
4) 4

Answer 1

A spring with mass can freely move in three dimensions (3D). Using the potential and kinetic energy formulas, we find that the total energy for the described system with two 4.0 kg masses and a compressed spring is 1.5 J.

Step-by-step explanation:

A spring with mass can move in three dimensions. This can be understood considering a simple model of a solid element where each atom is hypothetically connected to others by springs along the x, y, and z axes. Therefore, the spring can move in three spatial dimensions, corresponding to the different degrees of freedom in motion.

Worked Example

Let's consider a question related to the spring's movement and energy:

Two 4.0 kg masses are connected to each other by a spring with a force constant of 25 N/m and a rest length of 1.0 m. If the spring has been compressed to 0.80 m in length and the masses are traveling toward each other at 0.50 m/s (each), what is the total energy in the system?

To calculate the total energy in the system, we need to consider both the kinetic and potential energy. The potential energy stored in the compressed spring (U) is given by
`U = 1/2 * k * x^2`, where k is the force constant and x is the distance the spring is compressed from the equilibrium position. The kinetic energy (K) of each mass is given by
`K = 1/2 * m * v^2`.

Potential energy (U):

`U = 1/2 * 25 N/m * (1.0 m - 0.80 m)^2`

`U = 1/2 * 25 * 0.2^2`

`U = 0.5 J`

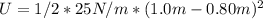
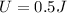
Kinetic energy (K) for both masses:

`K = 2 * (1/2 * 4.0 kg * (0.50 m/s)^2)`

`K = 2 * 1/2 * 4.0 * 0.25`

`K = 2 * 0.5`

`K = 1.0 J`

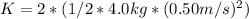
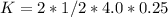
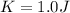
Therefore, the total energy in the system (E) is:

`E = U + K`

`E = 0.5 J + 1.0 J`

`E = 1.5 J`

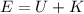
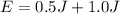
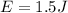
The correct answer is b.
`1.5 J`.