Question

Find the equation of a line shown.

Answer 1

⇒First in the diagram you can choose two points that will assist you in finding the the slope/gradient of the equation.

⇒Choosing two points from the diagram we get (1,1) and (2,3)

⇒Note you can use two points of your choice you would still get the same gradient/slope/

Gradient and slope are one and the same thing.

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) ) \\`

⇒
`m=(3-1)/(2-1) \\m=(2)/(1) \\m=2`

⇒In this case the gradient from the calculation is 2.

⇒The general equation to get the equation of a straight line is y=mx+c ,Note this is a straight line. we cans see that from the diagram.

I will use the point (1,1) in the p[lace (x,y) and m=2 to find the value of c

`1=2(1)+c\\1=2+c\\1-2=c\\c=-1`

As a results the equation of the straight line is y=2x-1

Answer 2

y = 2x - 1

Explanation:

In order to find the equation of a line, we need to first find the coordinates of two points that the line passes through. Using the coordinates, we then have to calculate the line's gradient. Finally, we need to find the y-intercept of the line and use it and the gradient to find the line's equation.

The y-intercept (c) of a line is the y-coordinate of the point where the line crosses the y-axis. From the graph, we can see that the line given passes through the y-axis where the y-coordinate is -1. Therefore the y-intercept is -1:

c = -1

From the graph shown, we can see that the line passes through the points (3, 5) and (1, 1). Therefore, we can calculate the gradient of the line using the following formula:

`m = (y_2 - y_1)/(x_2 - x_1)`,

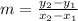where m is the line's gradient and (x₁, y₁) and (x₂, y₂) are points on the line.

Therefore, the gradient,

m =
`(5 - 1)/(3 - 1)`

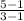
= 2

Now that we have the gradient and y-intercept of the line, we can use the following formula to find the equation of the line:

`\boxed{y = mx + c}`

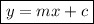
⇒ y = 2x + (-1)

⇒ y = 2x - 1

Therefore, the equation of the line shown is y = 2x - 1.