Question

Use the point-slope form to find the ewuation of the line through the points (-5,2) and (-2,6)

Answer 1

The equation of the line through the points (-5, 2) and (-2, 6) is
`y = (4)/(3)\cdot x +(26)/(3)`.

Explanation:

The point-slope form of the equation of the line is defined by this formula:

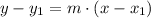`y-y_(1) = m\cdot (x-x_(1))` (1)

Where:

`x` - Independent variable.

`y` - Dependent variable.

`m` - Slope.

`x_(1)`,
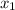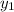`y_(1)` - Coordinates of the first point.

In addition, the slope of the line can be determined in terms of two distinct points:

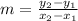`m = (y_(2)-y_(1))/(x_(2)-x_(1))` (2)

Where
`x_(2)`,
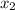`y_(2)` are the coordinates of the second point.

If we know that
`x_(1) = -5`,
`y_(1) = 2`,
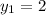`x_(2) = -2` and
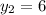`y_(2) = 6`, then the equation of the line is:

`m = (6-2)/(-2-(-5))`

`m = (4)/(3)`

`y-2 = (4)/(3)\cdot (x+5)`

`y = (4)/(3)\cdot x +(26)/(3)`

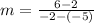
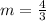
The equation of the line through the points (-5, 2) and (-2, 6) is
`y = (4)/(3)\cdot x +(26)/(3)`.