Question

Select the equation that contains the points, (-2, -2) and (4, 10).

Answer 1

Line containing points (-2,-2) and (4,10) is y-6=2(x-2) and the correct option is A.

The equation that contains the points (-2, -2) and (4, 10) is:

y - 6 = 2(x - 2)

This can be found using the point-slope form of linear equations, which is:

y - y_1 = m(x - x_1)

where m is the slope of the line and (x_1, y_1) is one point on the line.

To find the slope, we can use the two points that were given to us:

`m = (y_2 - y_1)/(x_2 - x_1) = (10 - (-2))/(4 - (-2)) = (12)/(6) = 2`

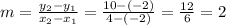
Now that we know the slope and one point on the line, we can plug them into the point-slope form to find the equation of the line:

y - (-2) = 2(x - (-2))

y + 2 = 2(x + 2)

y = 2x + 2 - 2

y = 2x - 2

Simplifying the equation, we get:

y - 6 = 2(x - 2)

Therefore, the equation that contains the points (-2, -2) and (4, 10) is y - 6 = 2(x - 2). So, the correct option is A.