Question

Multiply.
(2x + 4)(x - 4)

Answer 1

= 2x² - 4x - 16

Explanation:

(2x + 4)(x - 4)

= 2x*x + 2x*-4 + 4*x + 4* -4

= 2x² - 8x + 4x - 16

= 2x² - 4x - 16

Answer 2

`2x^2-4x-16`

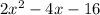
Explanation:

When multiplying two binomials we use the FOIL method, which consists of multiply the (f)irst terms by each other (in this case 2x and x), then the (o)utside terms (in this case 2x and -4), then the (i)nside terms (in this case 4 and x), and then finally the (l)ast terms (in this case 4 and -4)

I'll attach an image to demonstrate this a bit more clearly.

Once you get all these terms, you add them together, so we have:

`2x^2 - 8x+4x-16`

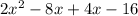
Combining like terms gives you the simplified equation:

`2x^2-4x-16`

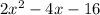
Expanding the FOIL method

This FOIL method is limited to multiplying binomials, but can be extended further by using the intuitive knowledge behind it.

You can generalize it by using the following:

`(a+b)(c+d)`

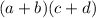
and then realize this can be expressed as, adding the expression (c + d), (a + b) times. Which can be expressed as such:

`(c + d)+(c+d)+(c+d)...\text{ (a + b) times}`

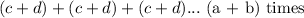
we can split this into

`(c+d)+(c+d)...\text{ a times}\ +(c+d)+(c+d)...\text{ b times}`

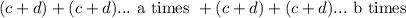
since if we add it "a" times, and then "b" times, we should get the same thing as adding it "a + b" times. This sounds a lot like multiplication... because it is! So we can rewrite the expression as such:

`a(c+d)+b(c+d)`

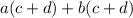
and then from here, we can use the distributive property:

`ac+ad+bc+bd`

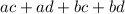
which is the same thing as the FOIL method, and is the reasoning behind it.

We can use this to multiply something in the form:

`(a+b+c)(d+e+f)\to a(d+e+f) + b(d+e+f) + c(d+e+f)`

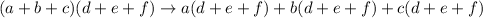
and then simply using the basic distributive property, and this method is essentially just the distributive property just a bit more complicated.

But using this knowledge we can multiply polynomials with any amount of terms.