Question

A 15kg box is motionless on the floor. The coefficient of static friction is 0.52 and coefficient of kinetic friction is 0.37.

Calculate the acceleration of box to justify your answer
Show your work

Answer 1

To calculate the acceleration of the box, we'll consider the forces acting on it. When the box is motionless, the static friction force
`(\(f_s\))` balances the applied force
`(\(F_{\text{applied}}\)).`

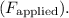
1. Static Friction Force
`(\(f_s\))`:

`\[ f_s \leq \mu_s \cdot N \]`

where
`\(\mu_s\)` is the coefficient of static friction, and N is the normal force.

2. Normal Force N:

In this case, when the box is on the floor, N is equal to the weight of the box mg, where m is the mass of the box (15 kg) and g is the acceleration due to gravity (approximately 9.8 m/s²).

3. Applied Force
`(\(F_{\text{applied}}\))`:

Assuming no other horizontal forces,

`\(F_{\text{applied}}\)` is the force required to overcome static friction:

`\[ F_{\text{applied}} = f_s \]`

Now, if
`\(F_{\text{applied}}\)` exceeds the maximum static friction force, the box starts moving, and we transition to kinetic friction.

4. Kinetic Friction Force
`f_k`:

Once the box is in motion,
`\(f_k = \mu_k \cdot N\)`, where
`\(\mu_k\)` is the coefficient of kinetic friction.

5. Acceleration a:

When the box is moving, the net force
`(\(F_{\text{net}}\))` is the difference between the applied force and the kinetic friction force:

`\[ F_{\text{net}} = F_{\text{applied}} - f_k \]`

Then,
`\(a = \frac{F_{\text{net}}}{m}\).`

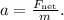
Now, we need to check whether the applied force is greater than the maximum static friction force. If so, the box moves, and we calculate the acceleration considering kinetic friction. If not, the box remains motionless, and the acceleration is zero.