Question

in an arcade game a 0.14 kg disk is shot across a frictionless horizontal surface by compressing it against a spring and releasing it. if the spring has a spring constant of 155 n/m and is compressed from its equilibrium position by 4 cm, find the speed with which the disk slides across the surface. answer in units of m/s.

Answer 1

Approximately
`1.3\; {\rm m\cdot s^(-1)}`.

Step-by-step explanation:

When an ideal spring with spring constant
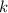`k` is displaced by
`x` from equilibrium, the elastic potential energy (
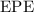`{\rm EPE}`) stored in the spring will be:

`\begin{aligned}{\rm PE} &= (1)/(2)\, k\, x^(2)\end{aligned}`.

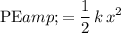If an object of mass
`m` is travelling at a speed of
`v`, the kinetic energy (
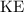`{\rm KE}`) of that object will be:

`\begin{aligned}{\rm KE} &= (1)/(2)\, m\, v^(2)\end{aligned}`.

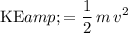Under the assumptions of this question, all the elastic potential energy (
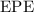`{\rm EPE}`) stored in the spring would have been turned into the kinetic energy (
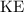`{\rm KE}`) of the disk.

Let
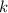`k` and
`x` denote the spring constant and displacement from equilibrium of this spring. Let
`m` and
`v` denote the mass and speed of the disk. Apply unit conversion and ensure that the displacement of the spring is in standard units (meters):
`x = 4\; {\rm cm} = 0.04\; {\rm m}`.

`{\rm EPE} = {\rm KE}`.

`\begin{aligned}(1)/(2)\, m\, v^(2) &= {\rm KE} = {\rm EPE} = (1)/(2)\, k\, x^(2)\end{aligned}`.

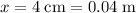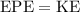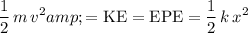Rearrange this equation to find the speed of the disk
`v`:

`\begin{aligned}v^(2) = (k\, x^(2))/(m)\end{aligned}`.

Since speed
`v \ge 0`:

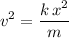`\begin{aligned}v &= \sqrt{(k\, x^(2))/(m)} \\ &= x\, \sqrt{(k)/(m)}\\ &= 0.04\; {\rm m} *\sqrt{\frac{155\; {\rm N \cdot m^(-1)}}{0.14\; {\rm kg}}} \\ &\approx 1.3\; {\rm m\cdot s^(-1)}\end{aligned}`.

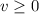(Note that
`1\; {\rm N \cdot m^(-1)} = 1\; {\rm (kg \cdot m\cdot s^(-2)) \cdot m^(-1)} = 1\; {\rm kg \cdot s^(-2)}`.)

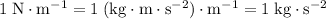Hence, the speed of the disk would be approximately
`1.3\; {\rm m\cdot s^(-1)}`.