The 99% confidence interval for the difference in mean DiNP concentration between people who ate fast food in the last 24 hours and those who didn't is 2.09 to 3.11 ng/mL. This means that there is a 99% chance that the true difference in mean DiNP concentration falls between these two values.
To find a 99% confidence interval for the difference in mean DiNP concentration between people who ate fast food in the last 24 hours and those who didn't, we can use the following formula:
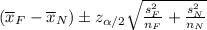
where:
 are the mean DiNP concentrations in the fast food and non-fast food groups, respectively
are the mean DiNP concentrations in the fast food and non-fast food groups, respectively
 are the standard deviations of DiNP concentrations in the fast food and non-fast food groups, respectively
are the standard deviations of DiNP concentrations in the fast food and non-fast food groups, respectively
 are the sample sizes of the fast food and non-fast food groups, respectively
are the sample sizes of the fast food and non-fast food groups, respectively
 is the critical value of the standard normal distribution for a 99% confidence interval, which is 2.576
is the critical value of the standard normal distribution for a 99% confidence interval, which is 2.576
Plugging in the values that were given in the question, we get the following confidence interval:
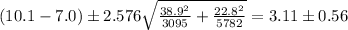
**Therefore, the 99% confidence interval for the difference in mean DiNP concentration between people who ate fast food in the last 24 hours and those who didn't is **2.09** to **3.11** ng/mL.
** This means that there is a 99% chance that the true difference in mean DiNP concentration falls between these two values.