Answer:
Perimeter = 18√3 = 18SQR(3)
Area = 27√3 = 27SQR(3)
Explanation:
The sides of a regular polygon are congruent.
Therefore, as the triangle is a regular polygon, it is an equilateral triangle since its sides (and interior angles) are congruent.
The interior angles of a triangle sum to 180°. Therefore, each interior angle of the equilateral triangle is 60°.
Therefore, the right triangle formed inside the equilateral triangle by the perpendicular bisectors is a 30-60-90 triangle with hypotenuse of 6 units.
The ratio of the side lengths of a 30-60-90 triangle is b : b√3 : 2b, where:
- b = shortest side opposite the 30° angle.
- b√3 = side opposite the 60° angle.
- 2b = longest side (hypotenuse) is opposite the right angle.
As the hypotenuse of the 30-60-90 right triangle is 6 units:

Therefore, the length of the longest leg of the right triangle is 3√3.
As this is half the length of one side of the equilateral triangle:

Heron's Formula allows us to find the area of a triangle in terms of its side lengths.
Heron's Formula
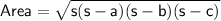
where:
- a, b and c are the side lengths of the triangle.
- s is half the perimeter.
Given:
- Each side length = 6√3 units
- Half perimeter = 9√3 units
Substitute these values into the Heron's formula to calculate the area of the equilateral triangle:
