Question

If point E exists such that its x-coordinate is 12 and ED is parallel to AC, then what is the y-coordinate of point E? Show how you arrived at your answer. (theres no diagram)

Answer 1

Point E's y-coordinate is 12, given parallel lines AC and ED, using slope and intercept method for line equations.

If line ED is parallel to line AC and point E has an x-coordinate of 12, we can determine the y-coordinate of point E by considering the slope of line AC.

Given that line AC is represented by points A(3, 5) and C(12, 8), we can calculate the slope of line AC using the formula:

`\[ \text{Slope} = \frac{\text{change in y}}{\text{change in x}} = (y_2 - y_1)/(x_2 - x_1) \]`

For line AC:

`\[ \text{Slope} = (8 - 5)/(12 - 3) = (3)/(9) = (1)/(3) \]`

Since ED is parallel to AC, both lines have the same slope. Therefore, the slope of line ED is also 1/3.

Given that the x-coordinate of point E is 12 and we know the slope of line ED is 1/3, we can use the slope-intercept formula y = mx + b to find the y-coordinate of point E.

Using point E (x = 12) and the slope m = 1/3, we rearrange the equation:

y = mx + b

`\[ y = (1)/(3) * 12 + b`

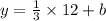
y = 4 + b

As the slope-intercept form indicates, the y-intercept b represents the y-coordinate of point E. Since the y-coordinate of point C is 8, and the slope m = 1/3, the y-coordinate of point E is 4 + 8 = 12. Therefore, the y-coordinate of point E is 12.